Dividing with Exponents
⇒ Definition of Negative Exponent
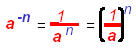
Note:
 They are reciprocals.
Example 1:
a)
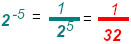 Notice that a negative exponent does not affect the sign of
the number.
b)
 |
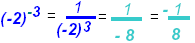→ Odd or Even exponents determine the sign. |
c)
|
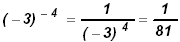
d)
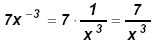
⇒ Division of powers with positive exponents:
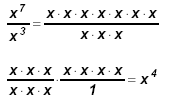
Notice that 7 − 3 = 4.
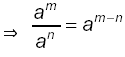or |
 |
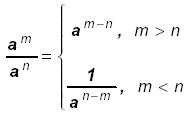Subtract the smaller exponent from the
larger exponent and put the resulting "power"
in the "place" of the larger "power".
Put a 1 in the numerator if the larger "power" is in the denominator.
|
Example 2:
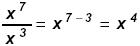→ Notice that 7 – 3 = 7 + (-3) = + 4
⇒ Operation of powers with negative exponents: Two methods:
Method 1: Follow the rule above carefully keeping the negative exponents in parens:
Example 3:
a)
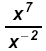 Since 7 > -2 work in the numerator:
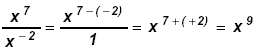
b)
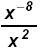 Since 2 > -8 work in the denominator:
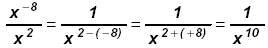
c)
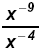 Since - 4 > - 9 work in the denominator:
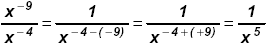
Method 2: To multiply or divide with "most" negative exponents, multiply both the numerator and the
denominator by the "reciprocal with positive power" and "neutralize the negative".
Example 4:
a)
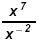 Since - 2 is
"most negative" multiply both by
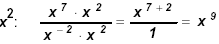
b)
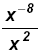 Since - 8
"most negative" multiply both by
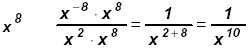
c)
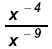 Since - 9 is
"most negative" multiply both by
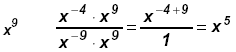
d)
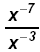 Since - 7 < -3, or - 7 is
"most negative" multiply by x7 ⇒
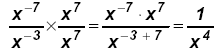or
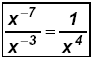
NOTE: Where there are several terms in the numerator and several terms in the
denominator
separate them into a product of fractions with "same letters"
Definition of Zero Exponent a 0 = 1
Note: The result of raising any base to the 0 exponent
will always be 1. (a ≠ 0)
Example 5:
1. (57x 9 y 32 z -25 )0 = 1
2.
|
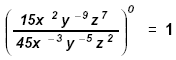
