Factoring simple expressions
Introduction
Before studying this material you must be familiar with the
process of removing brackets. This is because factoring can be
thought of as reversing the process of removing brackets. When we
factorise an expression it is written as a product of two or more
terms, and these will normally involve brackets.
1. Products and Factors
To obtain the product of two numbers they are multiplied
together. For example the product of 3 and 4 is 3×4 which equals
12. The numbers which are multiplied together are called factors.
We say that 3 and 4 are both factors of 12.
Example
The product of x and y is xy . The product of 5x and 3y is
15xy .
Example
x and 5 y are factors of 10xy since when we multiply x by 5 y
we obtain 10 xy .
( x + 1) and ( x + 2) are factors of x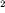 + 3 x + 2
because when we multiply ( x +1) by ( x + 2) we obtain x + 3 x + 2
because when we multiply ( x +1) by ( x + 2) we obtain x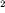 + 3 x + 2. + 3 x + 2.
3 and x -5 are factors of 3 x 15 because 3( x - 5) = 3 x - 15.
2. Common Factors
Sometimes, if we study two expressions to find their factors,
we might note that some of the factors are the same. These
factors are called common factors .
Example
Consider the numbers 18 and 12.
Both 6 and 3 are factors of 18 because 6 × 3 = 18.
Both 6 and 2 are factors of 12 because 6 × 2 = 12.
So, 18 and 12 share a common factor, namely 6.
In fact 18 and 12 share other common factors. Can you find
them?
Example
The number 10 and the expression 15 x share a common factor of
5.
Note that 10 = 5 × 2, and 15 x = 5 × 3 x . Hence 5 is a
common factor.
Example
3a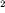 and 5a share a common factor of a since
and 5a share a common factor of a since
3a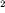 =
3 a × a and 5 a = 5 × a . Hence a is a common factor. =
3 a × a and 5 a = 5 × a . Hence a is a common factor.
Example
8x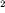 and 12 x share a common factor of 4 x since
and 12 x share a common factor of 4 x since
8x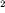 =
4x × 2x and 12x = 3x × 4x . Hence 4 x is a common factor. =
4x × 2x and 12x = 3x × 4x . Hence 4 x is a common factor.
3. Factoring
To factorize an expression containing two or more terms it is
necessary to look for factors which are common to the different
terms. Once found, these common factors are written outside a
bracketed term. It is ALWAYS possible to check your answers when
you factorize by simply removing the brackets again, so you
shouldn't get them wrong.
Example
Factorize 15 x + 10.
Solution
First we look for any factors which are common to both 15x and
10. The common factor here is 5. So the original expression can
be written
15 x + 10 = 5(3x ) + 5(2)
which shows clearly the common factor. This common factor is
written outside a bracketed term, the remaining quantities being
placed inside the bracket:
15 x + 10 = 5(3 x + 2)
and the expression has been factorized. We say that the
factors of 15 x + 10 are 5 and 3 x + 2. Your answer can be
checked by showing 5(3 x + 2) = 5(3 x ) + 5(2) = 15 x + 10
Exercises
Factorize each of the following:
1. 10x + 5y ,
2. 21 + 7x ,
3. xy - 8x ,
4 . 4 x -8xy
Answers
1. 5( 2x + y ),
2. 7(3 + x ),
3. x ( y - 8),
4. 4 x (1 - 2y ).
|