Horizontal Line Test
A function where each y-value (output) corresponds to exactly one x-value
(input) is called a one-to-one function. A one-to-one function has an
inverse function.
To determine if a function is one-to-one, we can use the horizontal line
test.
Note:Another way to think about a function that
is one-to-one is the following: Two
different input values always result in 2
different output values.
Procedure — To Determine if a Graph Represents a One-To-One Function
(Horizontal Line Test)
If you can draw a horizontal line anywhere through the graph of a
function and it intersects the graph at most once, then the graph
represents a one-to-one function.
Example 1
Given the graph of the function: f(x) = -2x + 4
a. Is f(x) a one-to-one function?
b. Does f(x) have an inverse?
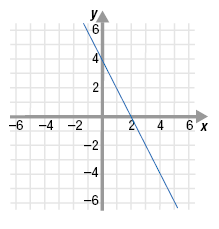
Solution
a. To determine if the function is one-to-one, use the horizontal line test.
Any horizontal line intersects the graph at most once. Thus, each
output corresponds to at most one input.
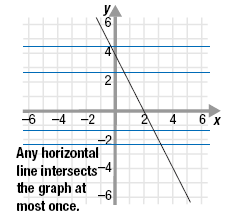
Therefore, f(x) = -2x + 4 is a one-to-one function.
b. Since the function is one-to-one, f(x) has an inverse.
Note:
Any linear function is one-to-one unless it
has the form f(x) = c, where c is a
constant.
The graph of f(x) = c is a horizontal line
and so it does not pass the horizontal line
test.
Example 2
Given the graph of the function: f(x) = -1(x - 3)2 + 4
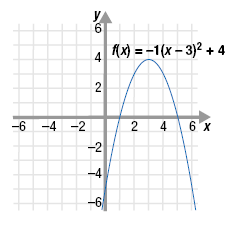
a. Is f(x) a one-to-one function?
b. Does f(x) have an inverse?
Solution
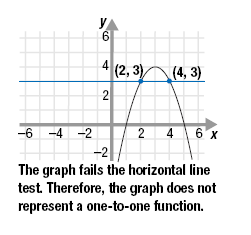
a. To determine if the function is one-to-one, use the horizontal line test.
Since a horizontal line may intersect the graph more than once, some
outputs correspond to more than one input.
For example, the y-value 3 corresponds to two x-values (2 and 4).
Therefore, this function is not one to one.
b. Since the function is not one-to-one, it does not have an inverse that is
a function.
|