Formulas
A formula is an equation that contains at least two variables. Sometimes it
is useful to solve a formula for one of the variables. That is, we write that
variable in terms of the other variables.
Example 1
The density, d, of an object can be found by dividing its mass, m, by its
volume, v.
That is,
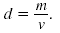
Solve this formula for v.
| Solution |
d |
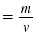 |
| Multiply both sides of the equation
by v, the denominator of the fraction.
|
v · d
|
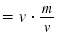 |
| Simplify. |
dv |
= m |
| Divide both sides by d. |
v |
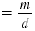 |
Thus,
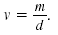
Note:
We could also solve for v by cross
multiplying.
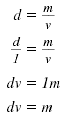
To check the solution, substitute
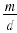 for v in the original equation. for v in the original equation.
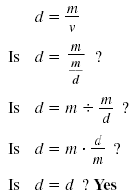
Example 2
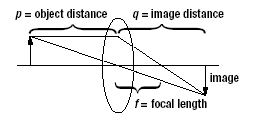
The focal length, f, of a thin lens is related to p, the distance between the
lens and the object, and q, the distance between the lens and the image,
by the formula:
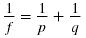
Solution
| Multiply each side by fpq, the LCD
of the fractions. |
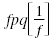 |
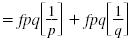 |
| Cancel common factors.
On the right side of the equation,
factor out f. |
pq pq |
= fq + fp = f(q + p) |
| Divide both sides by (q + p), the
coefficient of f.
|
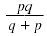 |
= f |
We leave the check to you.
|