Solving Rational Inequalities with a Sign Graph

The inequalities

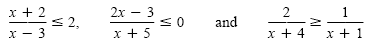
are called rational inequalities. When we solve equations that involve rational expressions, we usually multiply each side by the LCD. However, if we multiply each side of any inequality by a negative number, we must reverse the inequality, and when we multiply by a positive number, we do not reverse the inequality. For this reason we generally do not multiply inequalities by expressions involving variables. The values of the expressions might be positive or negative. The next two examples show how to use a sign graph to solve rational inequalities that have variables in the denominator.

Example 1

Solving a rational inequality

Solve 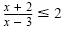and graph the solution set.

Solution

We do not multiply each side by x - 3. Instead, subtract 2 from each side to get 0 on the right:

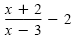	≤ 0
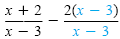	≤ 0	Get a common denominator.
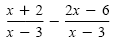	≤ 0	Simplify.
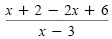	≤ 0	Subtract the rational expressions.
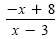	≤ 0	The quotient of -x + 8 and x - 3 is less than or equal to 0.

Examine the signs of the numerator and denominator:

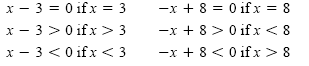
Make a sign graph as shown in the figure below.

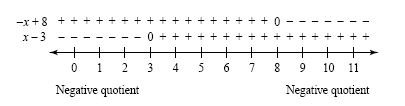
Using the rule for dividing signed numbers and the sign graph, we can identify where the quotient is negative or zero. The solution set is (-∞, 3) È [8, ∞). Note that 3 is not in the solution set because the quotient is undefined if x = 3. The graph of the solution set is shown in the next figure.

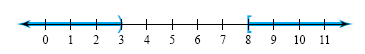
Helpful hint

By getting 0 on one side of the inequality, we can use the rules for dividing signed numbers. The only way to obtain a negative result is to divide numbers with opposite signs.

Caution

Remember to reverse the inequality sign when multiplying or dividing by a negative number. For example, x - 3 > 0 is equivalent to x > 3. But -x + 8 > 0 is equivalent to -x > -8, or x < 8.