Quotient Rule for Radicals
The power of a quotient rule is also valid for integral and rational exponents. This
rule allows us to write
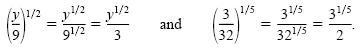
These equations can be written using radical notation as
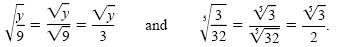
The power of a quotient rule (for the power 1/n) can be stated using radical notation.
When written with radicals, it is called the quotient rule for radicals.
Quotient Rule for Radicals
The nth root of a quotient is equal to the quotient of the nth roots. In symbols,
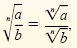
provided that all of the expressions represent real numbers and b
≠ 0.
Helpful hint
We could get by without the
rules for radicals. If we converted
every radical expression
to an exponential
expression, then we could
apply the rules for exponents.
However, it is simpler to learn a
few rules for radicals.
The quotient rule is used to simplify radicals by rewriting the root of a quotient
as the quotient of the roots.
Example 2
Using the quotient rule to simplify radicals
Simplify each expression.

Solution
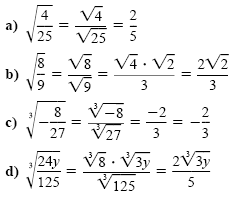
|